Linear programming (LP), LP relaxations, and rounding

14 Oct 2017

In this post, we’ll review linear systems and linear programming. We’ll then focus on how to use LP relaxations to provide approximate solutions to other (binary integer) problems that are NP-hard. Much of this post follows these randomized algorithms course notes [1].

Linear programming

One of the most basic ways of thinking of a problem is using linear equations. It turns out that linear problems are also easy to solve, whereas nonlinear problems are often hard to solve.

We can express a system of linear equations in matrix form as follows. Let \(A \in \mathbb{R}^{m \times n}\) be the matrix of coefficients, \(x \in \mathbb{R}^n \) a vector of variables (that we are interested in), \(b \in \mathbb{R}^m \) a vector of real numbers. We can express a system of \(m\) equations and \(n\) variables as the matrix equation \(Ax=b\).

We can also consider a system of linear inequalities by replacing some of the equalities with inequalities; i.e., \(Ax \geq b\), where \(\geq\) is a component-wise inequality. (Throughout this post, we will overload the \(\geq\) symbol and other inequalities to denote both component-wise inequality and scalar inequalities). The set of solutions is called the feasible region and is a convex polytope. In the figure below, the edges of the convex polytope are the linear inequalities, and any point in this feasible region satisfies this set of inequalities.

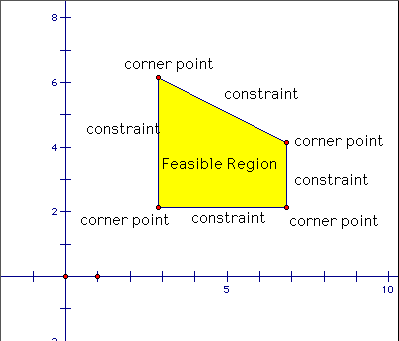(Image source: EMT6680)

We are often interested in optimizing (e.g., minimizing or maximizing) some linear function subject to a set of linear inequalities (i.e., constraints). This is called a linear program (LP) and in its most general form can be expressed as: \[ \text{minimize } c^\top x \] \[ \text{subject to } Ax \geq b, x\geq 0. \] Here \(c,b\) are known vectors of coefficients, \(A\) is a known matrix of coeffcients, and \(x\) is the unknown vector of the variables of interest.

(Fun history fact: linear programming was invented in 1939 by the Russian mathematician Leonid Kantorovich to optimize the organization of industrial production and allocation of a society’s resources.)

The optimal value of the objective function (that satisfies the constraints) \(x^*\) will be some vertex/corner/extreme point of the convex feasible region. The simplex algorithm is a method to enuerate the vertices one by one, decreasing the objective function at every step.

LP relaxations and approximation algorithms

In a number of problems, the unknown variables are required to be integers, which defines an integer program. Unlike linear programs, which can be solved efficiently, integer programs, while being more practical, are NP-hard. However, what we can do is relax these integer programs so that they are linear programs, by turning the integer constraints into linear inequalities.

Here we will look at three examples of LP relaxations. The first is an example that even though we solve the relaxed LP, we still end up with the integer solution. The other examples require some approximation achieved by rounding.

The assignment problem

We are interested in assigning \(n\) jobs to \(n\) factories, each job having some cost (raw materials, etc.). Let \(c_{ij}\) dnote the cost of assigning job \(i\) to factory \(j\), and let \(x_{ij}\) denote the assignment of job \(i\) to factory \(j\). Thus \(x_{ij}\) is a binary-valued variable and corresponds to a binary integer program.

To write the relaxed LP program, we turn this binary constraint into an inequality: \[ x_{ij} \geq 0 \text{ and } x_{ij} \leq 1,\] for all \(i,j \in [n] = \{1,\ldots,n\}\). But we also want each job to one factory and each factory to contain one job. So, we add the constraint \(\sum_{j=1}^n x_{ij}=1\) for each job \(i \in [n]\) to guarantee that each job \(i\) is only assigned to one factory, and the constraint \(\sum_{i=1}^n x_{ij}=1\) for all \(j \in [n]\) to ensure that each factory only gets a single job. This results in the relaxed LP program \[\text{minimize } \sum_{ij \in [n]} c_{ij} x_{ij}\] \[\text{subject to } 0 \leq x_{ij} \leq 1, \quad i,j \in [n] \] \[\sum_{j=1}^n x_{ij}=1, \quad i \in [n]\] \[\sum_{i=1}^n x_{ij}=1, \quad j \in [n]\] This LP results in variables that are all binary and actually solves the assignment problem.

However, in general, the solution of the LP produces a fractional solution, instead of an integer. Thus, to solve the original integer program, we can round the fractional solution to get an integer solution. We now discuss several examples where the LP relaxation gives us a fractional solution and how we might round these solutions (e.g., deterministically with a threshold or random rounding).

Approximate rounding solutions

Deterministic rounding

The simplest way to round a fractional solution to a binary one is by picking some threshold, e.g., 1/2, and rounding up or down depending on if variable is greater than or less than the threshold. We now consider the weighed vertex cover problem, which is NP-hard, and show that this deterministic rounding procedure gives us a ``good enough” approximate solution; i.e., with high probability, we get something within \((1+\epsilon)\) of the true value.

LP relaxation for the weighted vertex cover problem

In the weighted vertex cover problem, we are given a graph \(G = (V,E)\) and some weight \(w_i \geq 0\) for each vertex \(i\). A vertex cover is a subset of \(S \subset V\) such that every edge \(e \in E\) has at least one vertex \(v \in S\). The optimization problem is: find a vertex cover with minimum total weight. The relaxed LP program is: \[\text{minimize } f(x) = w^\top x \] \[\text{subject to } 0 \leq x \leq 1 \] \[ \quad x_i + x_j \geq 1, \quad\forall \{i,j\} \in E \] The first line is the objective, i.e., the total weight, where \(x_i\) is a variable that represents whether vertex \(i\) is in the cover \(S\). The second line gives the relaxed inequality, and the last line guarantees that we have a vertex cover, i.e., that for every each edge \(\{i,j\} \in E\), we have at least one vertex that is in the cover (either \(x_i=1\) and/or \(x_j=1\)).

How good is deterministic rounding?

Suppose \(O\) is the optimal value of this program, and let \(V\) be the minimum weight of the vertex cover problem. We have that \(O \leq V\) since every binary integer solution is also a fractional solution.

Now apply deterministic rounding to get a new set \(S\), where every vertex \(i\) with \(x_i \geq \frac{1}{2}\) is in the set, and otherwise not in \(S\). This produces a vertex cover because for every edge \(\{i,j\} \in E\), we know that we must satisfy the constraint \(x_i + x_j \geq 1,\) which implies that \(x_i \geq \frac{1}{2}\) and\or \(x_j \geq \frac{1}{2}\).

Since the optimal value at the solution is \[O = \sum_{i=1}^n w_i x_i,\] when we apply the rounding, we only pick the vertices that are greater than \(\frac{1}{2}\), and so the resulting weight of \(S\) is at most twice the weight of the optimal value of the LP, i.e., \(2O\). Thus, we have a resulting vertex cover with cost within a factor of 2 of the optimum cost.

Randomized rounding

Instead of the deterministic thresholding procedure, we could consider a randomized rounding procedure. One simple randomized rounding procedure is round the fractional variable \(x_i\) up to 1 with probability \(x_i\) (and down with probability \(1-x_i\)). The rounded variable therefore has expectation \(x_i\), and by linearity, the expectation of a linear constraint (i.e., \(c^\top x = d\)) that the fractional \(x\) satisfies is, in expectation, satisfied by the rounded variable.

We will consider using this randomized rounding procedure for the MAX-2SAT problem. In this problem, we have \(n\) boolean variables \(x_1,\ldots,x_n\), and a set of clauses of two literals \(y \vee z\), where each literal is either some \(x_i\) or its negation \(\neg x_i\). The goal is to find an assignment that maximizes the number of satisfied clauses \(y \vee z\) (i.e., the clauses is true).

LP relaxation for MAX-2SAT

For this problem, we will form the following LP relaxation. Let \(J\) be a set of clauses, and \(y_j = (y_{j1}, y_{j2})\) the literals in clause \(j\); and so \(y_{j1}\) is \(x_i\) if the first literal in clause \(j\) is \(x_i\), and \(1-x_i\) if it is the negation.

We will define the variable \(z_j\) for each clause \(j\), where \(\begin{align} z_j = \begin{cases} 1 &\text{ if clause } j \text{ satisfied} \\ 0 &\text{ otherwise}. \end{cases} \end{align}\)

Thus, taking the sum over all \(z_j\) gives us the total number of satisfied clauses, and thus defines our objective function.

So, we can express this as the relaxed LP

\[\begin{align} \text{maximize } \sum_{j \in J} & z_j \\ \text{subject to } 1 \geq x &\geq 0 \\ 0 \leq z &\leq 1 \\ \mathbf{1}^\top y_j &\geq z_j \qquad \forall j, \end{align}\]

where \(\mathbf{1}:=[1,1]^\top\). Here \(x\) and \(z\) are both relaxed to be fractional, and the last line ensures that the logic of the clauses holds.

How good is randomized rounding?

Now let \(O\) be the optimal value of the this LP, and \(M\) denote the number of clauses satisfied by the best assignment in MAX-2SAT. We have that \( M \leq O\).

Now apply randomized rounding to the fractional solution to get the 0/1 assignment. It turns out that the expected number of clauses satisfied is at least \(\frac{3}{4}\) the optimal value of the LP \(O\).

We can have \(j\) clauses that are either of size 1 or size 2. If the clause is of size 1, \(x_r\), then the probability it is satisfied is \(x_r\). But we must have \(x_r \geq z_j\) from the constrainst, so the probability this clause is satisfied is at least \(\frac{3}{4}z_j\).

Now suppose we have a clause of size 2, e.g., \(x_r \vee x_s\). Note that the probability of success after randomized rounding is 1 minus the product of if both are 0, i.e., \[1 - (1-x_r)(1-x_s) = x_s + x_r - x_r x_s,\] but since we know from the constraint that \[z_j \leq x_r + x_s, \] we can write that the probability of success is at least \(\begin{align} x_s + x_r - x_r x_s &\geq x_r + x_s - \frac{1}{4}(x_r + x_s)^2 \\ &\geq z_j - \frac{1}{4}z_j^2 \geq \frac{3}{4} z_j. \end{align}\)

So, since all clauses individually are satisfied with probability at least \(\frac{3}{4}z_j\), by linearity of expectation, the expected number of clauses satisfied is at least \(\frac{3}{4} O\).

Summary

Here we have discussed approximate solutions to integer programs via LP relaxations and two simple rounding schemes. Other problems likely require more complicated rounding schemes. Here we discussed two problems where simple deterministic and random rounding give easy to analyze approximate solutions are are within a constant factor of the solution. Many more rounding schemes and algorithms can be found in Williamson and Shmoys (2010) [2].

Resources

1. Arora, Kothari, Weinberg (2017). Advanced Algorithm Design Notes

2. Williamson and Shmoys (2010). Design of Approximation Algorithms